반응형
관련글
그래프 관련 포스팅은 여기를 참조
DFS 관련 포스팅은 여기를 참조
BFS 관련 포스팅은 여기를 참조
1. 개요
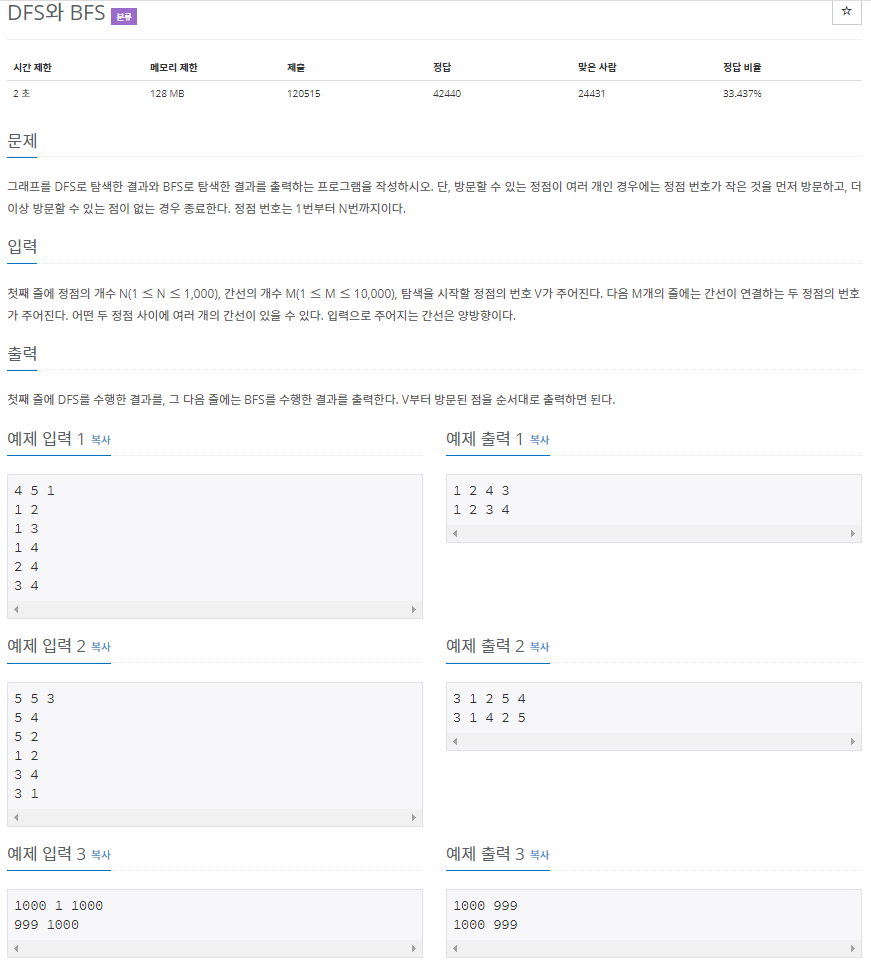
문제의 링크는 여기를 참조
문제의 내용은 아래의 더보기를 클릭하여 참조
그래프 형태를 DFS, BFS로 탐색한 결과를 각각 출력하는 문제.
2. 풀이
단순히 양방향 그래프를 DFS, BFS 방식으로 탐색하여 그 결과를 출력하는 방식이다.
이 문제는 인접 정점 중 더 작은 번호를 우선 탐색해야 하기 때문에 인접 리스트로 구현 시, 각 정점과 인접한 정점들의 리스트를 정렬하여 저장하면 작은 번호를 우선 탐색할 수 있게 된다.
DFS, BFS의 개념은 상단의 링크를 참조
3. 코드
아래의 코드를 통해 정답을 알아보자.
import java.io.*;
import java.util.*;
public class Main{
static StringBuilder sb;
static ArrayList<Integer> graph[];
static int n;
static int m;
static boolean visited[];
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
sb = new StringBuilder();
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
int start = Integer.parseInt(st.nextToken());
graph = new ArrayList[n+1];
for(int i=0; i <= n; i++){
graph[i] = new ArrayList<>();
}
for(int i=0; i < m; i++){
st = new StringTokenizer(br.readLine());
int v1 = Integer.parseInt(st.nextToken());
int v2 = Integer.parseInt(st.nextToken());
// 양방향 접촉
graph[v1].add(v2);
graph[v2].add(v1);
}
// 숫자가 작은 것부터 우선 방문하기 위해 정렬을 수행함
for(int i=1; i <= n; i++){
Collections.sort(graph[i]);
}
// DFS 방식으로 탐색
visited = new boolean[n+1];
dfs(start);
sb.append("\n");
// BFS 방식으로 탐색
visited = new boolean[n+1];
bfs(start);
System.out.println(sb);
br.close();
}
// DFS 방식 탐색. 재귀로 구현, 이 상태에서는 Stack 사용 시 작은 숫자부터 되지 않음
// Stack 사용을 원하면 코드를 변경해야 함
private static void dfs(int curr){
if(visited[curr]){
return;
}
visited[curr] = true;
sb.append(curr).append(" ");
for(int next : graph[curr]){
if(!visited[next]){
dfs(next);
}
}
}
// BFS 방식 탐색. Queue를 이용하여 탐색 수행
private static void bfs(int curr){
Queue<Integer> q = new LinkedList<>();
q.add(curr);
visited[curr] = true;
while(!q.isEmpty()){
int now = q.poll();
sb.append(now).append(" ");
for(int next : graph[now]){
if(!visited[next]){
visited[next] = true;
q.add(next);
}
}
}
}
}
읽어주셔서 감사합니다. 오류가 있으면 지적해주시면 반영하겠습니다.
반응형
'알고리즘 풀이(Problem Solving) > 그래프, 트리' 카테고리의 다른 글
| 알고리즘 풀이 - 백준 4963(섬의 개수, 그래프(DFS, BFS)) (0) | 2021.03.01 |
|---|---|
| 알고리즘 풀이 - 백준 2667(단지번호붙이기, 그래프(DFS, BFS)) (0) | 2021.02.27 |
| 알고리즘 풀이 - 백준 1707(이분 그래프, 그래프(DFS, BFS)) (0) | 2021.02.27 |
| 알고리즘 풀이 - 백준 11724(연결 요소의 개수, 그래프(DFS, BFS)) (0) | 2021.02.27 |
| 알고리즘 풀이 - 백준 13023(ABCDE, 그래프(DFS)) (0) | 2021.02.27 |