반응형
관련글
그리디 알고리즘 관련 포스팅은 여기를 참조
1. 개요
문제의 링크는 여기를 참조
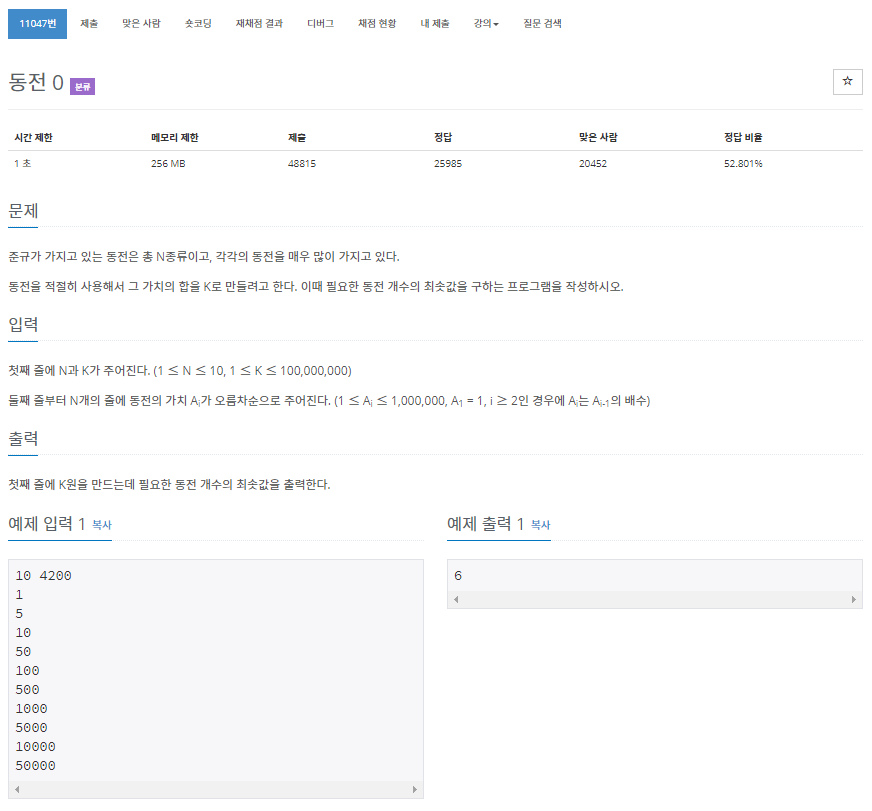
문제의 내용은 아래의 더보기를 클릭하여 참조
N개의 서로 다른 종류의 동전으로 K라는 숫자를 만들 수 있을 때, 최소의 개수로 만드는 경우의 수를 구하는 문제
2. 풀이
이 문제는 대표적인 쉬운 그리디 알고리즘으로 풀 수 있는 문제이다.
동전들이 N개 있을 때, $A_n 은 A_{n-1}$의 배수이기 때문에 동일한 숫자를 큰 단위의 동전으로 만드는 것은 작은 동전으로 만드는 경우보다 무조건 더 적은 수의 동전이 필요하다.
예를 들어, 1,000을 만들고 싶을 때, 동전이 2가지가 있는데 각 동전이 500, 1000원 짜리라고 생각해보자.
이 경우에 1,000원 짜리 동전은 1개면 되지만 500원짜리 동전은 2개가 필요하다. 그 어떤 경우에도 큰 동전의 수보다 더 적게 만드는 것은 불가능하다.
따라서, 큰 동전부터 시작하여 숫자를 만들기 시작하여 전체 숫자를 만들기 위해 필요한 동전의 수를 구하면 간단히 해결이 가능하다.
3. 코드
아래의 코드를 통해 정답을 알아보자.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main{
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int[] coins = new int[n];
// 정렬되어 나타나므로 뒤에서부터 저장한다.
for(int i=n-1; i >= 0; i--){
coins[i] = Integer.parseInt(br.readLine());
}
// 제일 큰 단위의 동전으로 시작하여 값을 메꾼다.
int ans = 0;
for(int i=0; i < n; i++){
// 현재 k가 동전보다 더 크거나 같은 경우에만 현재 동전을 쓸 수 있다.
if(coins[i] <= k){
// 사용된 동전의 수를 추가
ans += (k / coins[i]);
// 나머지 만큼은 추가 연산해야 하므로 빼준다.
k %= coins[i];
}
// 0원이 되었다면 그만둔다.
if(k == 0) break;
}
System.out.println(ans);
br.close();
}
}
읽어주셔서 감사합니다. 오류가 있으면 지적해주시면 반영하겠습니다.
반응형
'알고리즘 풀이(Problem Solving) > 그리디(Greedy Algorithm)' 카테고리의 다른 글
| 알고리즘 풀이 - 백준 1285(동전 뒤집기, 그리디(Greedy)) (0) | 2021.04.12 |
|---|---|
| 알고리즘 풀이 - 백준 2138(전구와 스위치, 그리디(Greedy)) (2) | 2021.04.12 |
| 알고리즘 풀이 - 백준 1080(행렬, 그리디(Greedy)) (0) | 2021.04.12 |
| 알고리즘 풀이 - 백준 11399(ATM, 그리디(Greedy)) (0) | 2021.04.11 |
| 알고리즘 풀이 - 백준 1931(회의실 배정, 그리디(Greedy)) (0) | 2021.04.11 |