전체 정렬 개요의 설명은 여기를 참조
Bubble / Selection / Insertion 정렬의 설명은 여기를 참조
Shell 정렬의 설명은 여기를 참조
Merge 정렬의 설명은 여기를 참조
Quick 정렬의 설명은 여기를 참조
Heap 정렬은 우선순위 큐에서 사용하는 정렬이므로 해당 포스팅 여기를 참조
Counting 정렬의 설명은 여기를 참조
Radix 정렬의 설명은 여기를 참조
Bucket 정렬의 설명은 여기를 참조
1. Topological Sort(위상 정렬)
위상 정렬은 순서가 있는 작업을 해야할 때 그 순서를 임의로 설정할 수 있도록 정렬하는 알고리즘이다. 예를 들어서 A라는 작업을 한 뒤에 B라는 작업을 해야한다고 생각하자.
그 경우, 작업 순서는 A → B 가 될 것이다. B → A는 성립할 수 없다. 따라서, 각 데이터가 어떤 행위 또는 값을 저장하고 있고 탐색에 따른 순서를 지정하고 싶을 때, 우리는 위상 정렬을 사용할 수 있다.
아래와 같은 예시를 한 번 보자.

입학을 해서 졸업 까지 가기 위해 위와 같은 절차를 거쳐야 할 수 있다. 여기서 중요한 것은 졸업에서 입학 또는 이전의 단계로 다시 갈 수 없다는 것이다.
즉, 전체 정렬에 Cycle이 있어서는 안된다. 위 그림은 그래프 형태의 자료구조를 차용하고 있음을 알 수 있고, 방향성이 있지만 Cycle은 없다.
즉, 위상 정렬은 DAG(Directed Acyclic Graph) 형태로 그려낼 수 있다.
(그래프에 대한 설명은 여기를 참조)
위상 정렬은 그래프 탐색의 일종이기 때문에 시간 / 공간복잡도에 대해서만 표기한다.
| 알고리즘 | 시간복잡도(최상) | 시간복잡도(평균) | 시간복잡도(최악) | 공간복잡도 |
| 위상 정렬 | O(V+E) | O(V+E) | O(V+E) | O(V) |
V는 Vertex로 정점을 의미하며, E는 Edge로 간선을 의미한다. 따라서, 정점과 간선의 수에 따라 시간복잡도가 결정되고, 구현 시, Stack / Queue 등 별도의 저장 공간이 정점의 수만큼 필요하기에 공간복잡도도 위와 같이 결정된다.
2. 정렬 과정(Queue 사용 시)
위상 정렬의 정렬 과정을 알아보자. 예를 들어 다음과 같은 그래프가 있다고 가정하자.
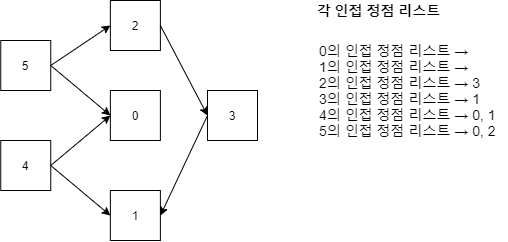
그래프를 구현 시에는 각각의 정점에는 내차수 값을 설정할 수 있다. 혹은 진입 차수라고도 부르는데, 다른 정점이 자신을 가리킬 때, 자신의 내차수 값이 증가한다.
우선 Queue를 이용하여 구현 시에 어떻게 동작하는지 알아보자.
Kahn's 알고리즘을 사용해 구성할 수 있다. 동작 원리는 다음과 같다.
① 내차수 값이 0인 정점을 모두 큐에 넣는다.
② 큐에서 하나씩 빼고, 빠진 정점이 가리키던 정점의 내차수 값을 1씩 빼준다.
③ 내차수 값이 1씩 빠진 정점 중, 내차수 값이 0이 된 정점을 큐에 넣는다.
④ 모든 정점을 순회할 때까지 ②, ③을 반복한다.
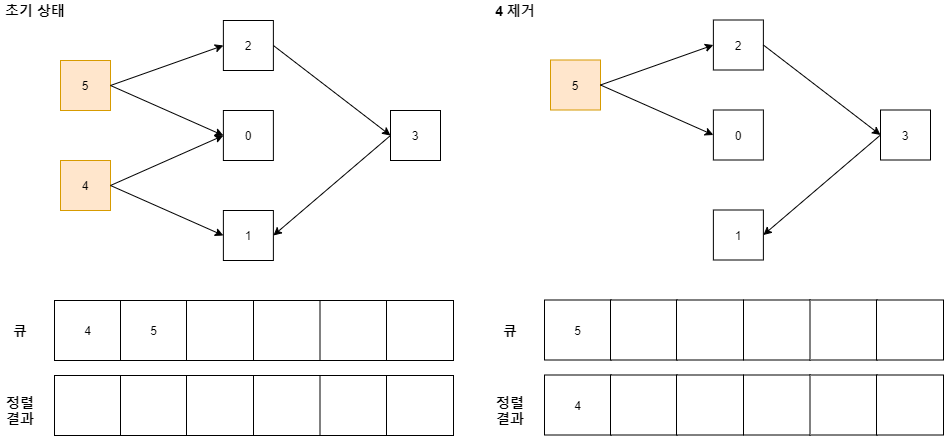
초기에는 내차수가 0인 값, 즉 자신을 가리키는 정점이 0인 정점을 모두 큐에 넣는다.(여기서는 4, 5)
이후, 큐에서 하나씩 빼고, 빠진 정점이 가리키던 다른 정점들의 내차수 값을 1씩 줄이고 그 중 다시 내차수 값이 0이 된 정점을 큐에 넣는다.
데이터 4를 가진 정점이 가리키는 정점은 0과 1이 있고, 0은 5도 자신을 가리키고 있기 때문에 내차수 값이 1이고 1도 3이 자신을 가리키고 있어서 내차수 값이 1이므로 추가할 것이 없다.
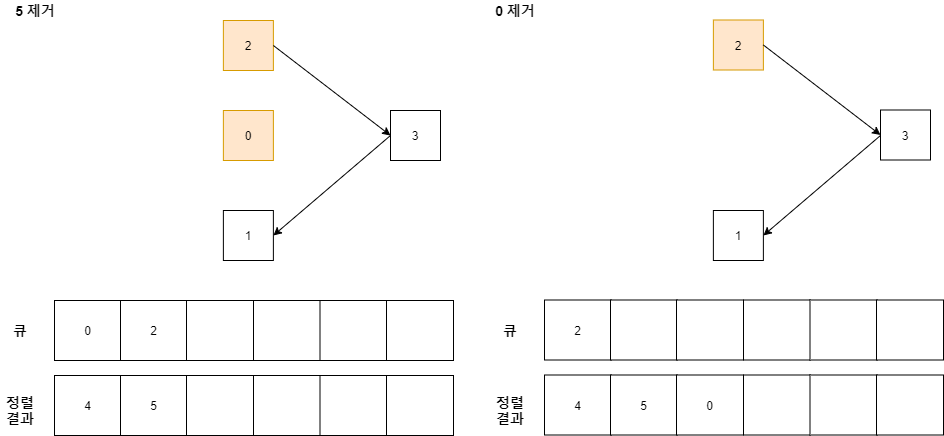
이 과정을 동일하게 반복하고 모든 정점을 순회할 때까지 지속한다.
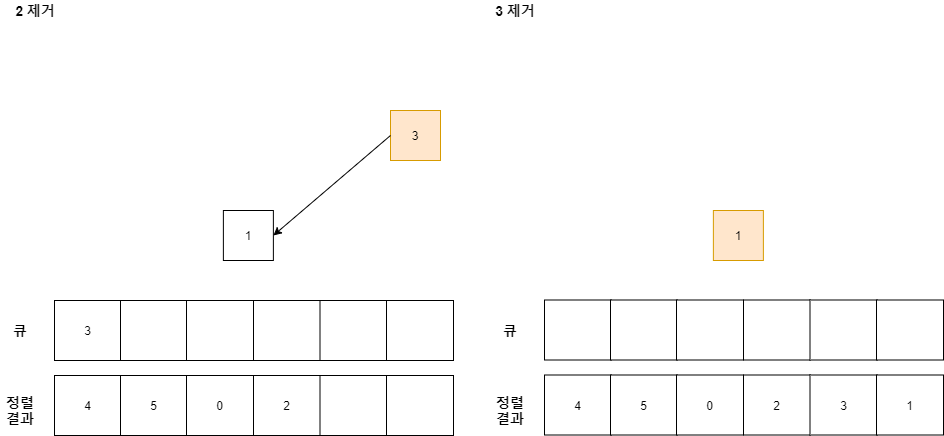
이와 같이 하나의 위상 정렬 결과가 만들어질 수 있다. 참고로, 위상 정렬 결과는 어떻게 최초에 그래프를 구현하느냐에 따라 전체 정렬 결과는 다를 수 있다.
3. 정렬 과정(Stack 사용 시)
Stack을 이용해서도 구현할 수 있는데, Stack을 이용할 때는 어떻게 동작할까? 알아보자. 원리는 다음과 같다.
기본적으로 DFS(Depth-First Search, 그래프 순회의 방식 중 하나)의 개념을 사용한다.(추후 포스팅 예정)
① List 형태의 그래프이므로 처음부터 순회를 시작한다. Boolean 배열로 순회 완료 여부를 표기한다.
② 각 정점을 순회하며 재귀호출을 통해 자신이 가리키는 정점을 순회한다. (각 정점 방문 완료 처리도 진행)
③ 더 이상 가리키는 정점이 없어 순회가 불가하면 현재 정점부터 차례로 Stack에 넣는다.
④ 위 과정을 반복 후 Stack에서 하나씩 꺼낸다.

인접 리스트 형태로 구현했다면 반드시 0부터 순회하는 것은 아닐 수 있다. 하지만 편의를 위해 0부터 차례로 순회했다고 생각한다.
자신이 가리키는 것이 순서에 있어 뒤이기 때문에 그것들을 모두 스택에 넣고 마지막에 자신을 넣는다. 기 방문 상태라면 넣지 않는다.
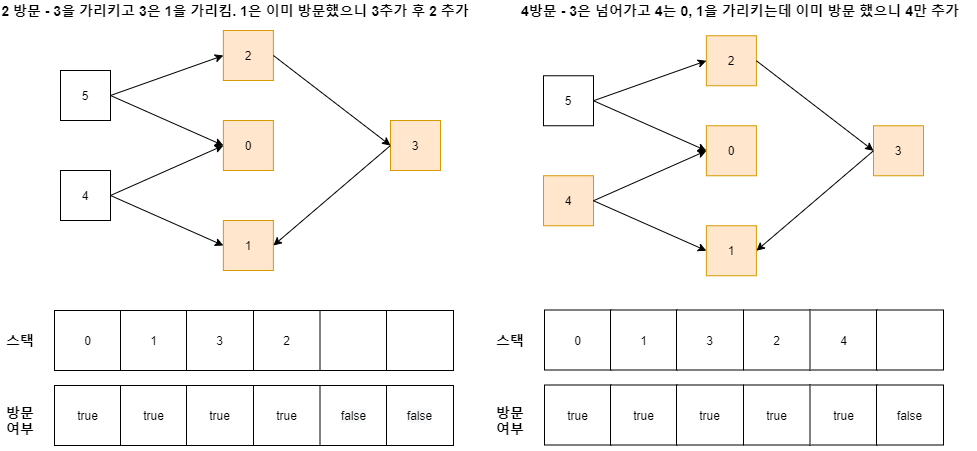
2 방문 시, 2가 가리키는 순서대로 추가한 후 2를 추가한다. 2를 방문했을 때, 3이 이미 방문 완료이므로 4로 넘어간다.
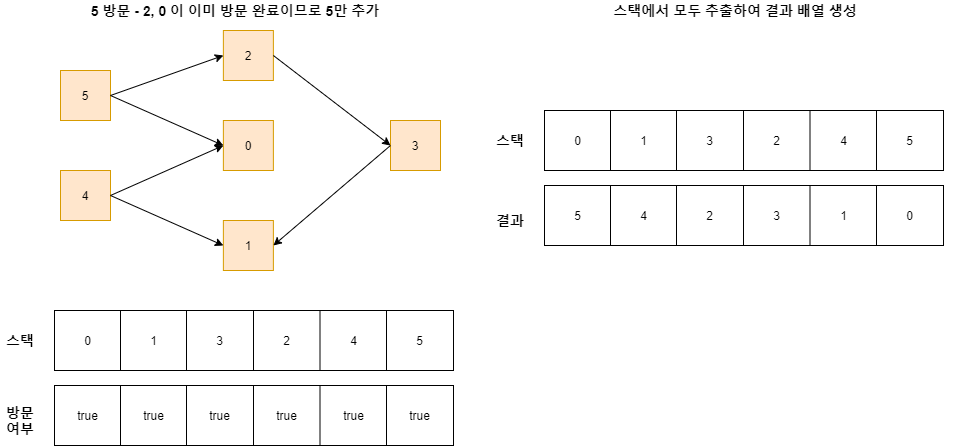
스택에 모두 넣었고 순회를 완료했다면 스택에서 모두 빼서 결과를 만들 수 있다.
기존 큐를 이용한 방식과 결과가 다른데, 위상 정렬은 Hamiltonian Path를 찾지 못한다면 둘 이상의 결과를 가질 수 있다.
※ Hamiltonian Path란?
해밀턴 경로라고 부르는데, 무방향 / 방향 그래프 상에서 모든 정점을 단 한 번만 지나는 경로를 의미한다. 그래프 G(V, E)내의 임의의 정점에서 출발해 한 번씩만 방문하고 다시 출발 정점으로 돌아오지 않는 경우를 의미한다.
아일랜드 수학자 윌리엄 로원 해밀턴의 이름을 본따 지어졌다.
※ Hamiltonian Cycle 이란?
모든 정점을 한 번씩 지나는 경로를 갖는 Cycle을 의미한다. 즉, 출발 정점과 도착 정점이 같고 중간의 모든 정점을 포함하는 경로를 의미한다.
Hamiltonian Cycle을 찾는 문제를 NP-Complete 이라고 부른다.
방향 그래프 상에 Hamiltonian Path가 있고 Hamiltonian Cycle이 없다면 위상 정렬은 Unique하다.
즉, 한 번의 경로에 모든 정점을 1회씩 방문할 수 있고 순환이 없다면 위상 정렬은 Unique하다고 볼 수 있다.
3. Cycle 탐지하기
DAG(Directed Acyclic Graph)는 Cycle이 없는 방향 그래프여야 한다. DAG가 성립한다는 의미는 최소 하나의 정점은 내차수(In-Degree)가 없고, 최소 하나의 정점이 외차수(Out-Degree)가 없어야 한다.
Cycle이 없다는 것은 모든 정점 간 경로가 유한하다는 의미인데, Cycle이 있는 경우, 무한한 경로가 발생할 수 있게 되기 때문이다.
그렇다면, 위 성질을 이용해 위상 정렬을 수행하다가 Cycle이 있는지를 체크하는 코드를 구현할 수도 있을 것이다. 어떻게 가능할까?
① 큐(Queue)를 이용한 구현 시
큐를 이용해 구현 시, 위에서 쓴 내용을 다시 잘 생각해보자. 기본적으로 처음부터, 모든 정점을 순회해 내차수 값이 0인 정점을 큐에 넣고 다시 큐에서 하나씩 빼며 해당 정점이 가리키는 모든 정점의 내차수를 감소시킨 뒤, 0이 되면 큐에 넣었다.
이 과정을 큐가 빌 때까지 진행하는데, 큐가 비었다는 것은 더 이상 순회를 못 한다는 의미와 같다.
그런데, Cycle이 있다면 내차수 값이 0이 되는 것이 절대 불가능하다. 서로가 서로를 가리키는 현상이 발생하여 아무도 자기 자신을 가리키지 않는 내차수 0이 되는 경우가 발생할 수 없는 것이다.
따라서 애초에 Cycle의 안쪽에 있던 정점들은 큐에 넣어질 수 없으니, 전체 정점의 수와 큐를 순회하며 정점을 꺼낸 수를 비교해서 다르다면 Cycle이 있는 것이다.
이를 어떻게 구현하는지 아래의 4. 코드로 구현하기 부분에서 확인해보자.
② 스택(Stack)을 이용한 구현 시
스택을 이용해 구현 시, 원리를 잘 생각해보자. 임의의 한 출발점에서 시작해 방문 완료 처리를 하고 그 정점이 가리키는 정점을 방문하여 또 방문 완료 처리하고 이 과정을 더 이상 추가로 가리키는 경우가 없을 경우에 스택에 재귀로 돌아가며 하나씩 넣게 된다.
즉, 스택에 넣는 과정이 완료되기 전에는 재귀 호출에 의해 코드의 로직 상에 쌓여서 대기하는 상태가 된다. 이 의미는 방문 완료 처리를 했으며 현재 방문이 진행중이라는 의미다.
그러므로, 방문 진행 중임을 표기하는 beingVisited 배열을 하나 더 만들어서 이 값이 true인데 재방문을 했다면 Cycle이 있는 상태라고 인지할 수 있다.
이를 어떻게 구현하는지 아래의 4. 코드로 구현하기 부분에서 확인해보자.
4. 코드로 구현하기
① Queue를 이용한 Topological Sort 구현
package com.test;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
public class Graph {
public static void main(String[] args){
int n = 6;
// Cycle이 없는 경우
Graph graph = new Graph();
graph.create_graph(n);
graph.add_edge(2, 3);
graph.add_edge(3, 1);
graph.add_edge(4, 0);
graph.add_edge(4, 1);
graph.add_edge(5, 0);
graph.add_edge(5, 2);
int[] result = new int[n];
boolean sort_result = graph.topological_sort(result);
if(sort_result){
for(int i : result){
System.out.print(i + ", ");
}
System.out.println();
} else {
System.out.println("Cycle이 발생했습니다!");
}
// Cycle이 있는 경우
graph = new Graph();
graph.create_graph(n);
graph.add_edge(2, 3);
graph.add_edge(3, 1);
graph.add_edge(4, 0);
graph.add_edge(4, 1);
graph.add_edge(5, 0);
graph.add_edge(5, 2);
// 1이 5를 가리키는 상황을 추가!
// 이 부분에 의해 1 - 5 - 3이 서로 Cycle을 이루게 됨!
graph.add_edge(1, 5);
result = new int[n];
sort_result = graph.topological_sort(result);
if(sort_result){
for(int i : result){
System.out.print(i + ", ");
}
System.out.println();
} else {
System.out.println("Cycle이 발생했습니다!");
}
}
private int V; // 정점의 개수
private int E; // 간선의 개수
private ArrayList<ArrayList<Integer>> adj; // 그래프를 표현하는 인접 리스트
private int[] indegree;
// 임의로 그래프 생성하는 Method
// 그래프 생성은 상황에 따라 유연하게 구현하면 됨
public void create_graph(int V){
this.V = V;
this.adj = new ArrayList<>();
this.indegree = new int[V]; // 내차수값 설정을 위한 배열
// 리스트 내에 리스트를 생성
// 인접 리스트 방식의 그래프 구현
for(int i=0; i < V; i++){
this.adj.add(new ArrayList<>());
}
}
// Graph의 정점 간 연결을 수행하는 Method
public void add_edge(int source, int target){
if(source > this.V || target > this.V){
throw new NullPointerException();
}
// source에 target으로의 방향성을 갖는 간선 추가
this.adj.get(source).add(target);
this.indegree[target]++; // 내차수값 증가(target이 대상이므로 target에 추가)
this.E++; // 간선 개수 ++, 사실 여기서는 쓰이진 않음.
}
// 위상 정렬을 수행하는 method
public boolean topological_sort(int[] result){
Queue<Integer> q = new LinkedList<>();
// 내차수가 0 인 것들을 모두 q에 삽입한다.
for(int i=0; i < this.V; i++){
if(this.indegree[i] == 0){
q.offer(i);
}
}
// 결과 배열에 저장하기 위해 index값을 설정, 전체 정점 개수와 비교할 수 있는 값도 됨
int index = 0;
while(!q.isEmpty()){
int current = q.poll();
result[index++] = current;
for(int target : this.adj.get(current)){
this.indegree[target]--;
if(this.indegree[target] == 0){
q.add(target);
}
}
}
// index와 V의 값 비교, 다르다면 Cycle이 있는것
if(this.V != index) {
return false;
}
return true;
}
}
결과는 다음과 같다.
4, 5, 0, 2, 3, 1,
Cycle이 발생했습니다!
Process finished with exit code 0
② Stack을 이용한 Topological Sort 구현
package com.test;
import java.util.ArrayList;
import java.util.Stack;
public class Graph {
public static void main(String[] args){
int n = 6;
Graph graph = new Graph();
graph.create_graph(n);
graph.add_edge(2, 3);
graph.add_edge(3, 1);
graph.add_edge(4, 0);
graph.add_edge(4, 1);
graph.add_edge(5, 0);
graph.add_edge(5, 2);
int[] result = new int[n];
boolean sort_result = graph.topological_sort(result);
if(sort_result){
for(int i : result){
System.out.print(i + ", ");
}
System.out.println();
} else {
System.out.println("Cycle이 발생했습니다!");
}
// Cycle이 있는 경우
graph = new Graph();
graph.create_graph(n);
graph.add_edge(2, 3);
graph.add_edge(3, 1);
graph.add_edge(4, 0);
graph.add_edge(4, 1);
graph.add_edge(5, 0);
graph.add_edge(5, 2);
// 1이 5를 가리키는 상황을 추가!
// 이 부분에 의해 1 - 5 - 3이 서로 Cycle을 이루게 됨!
graph.add_edge(1, 5);
result = new int[n];
sort_result = graph.topological_sort(result);
if(sort_result){
for(int i : result){
System.out.print(i + ", ");
}
System.out.println();
} else {
System.out.println("Cycle이 발생했습니다!");
}
}
private int V; // 정점의 개수
private int E; // 간선의 개수
private ArrayList<ArrayList<Integer>> adj; // 그래프를 표현하는 인접 리스트
private int[] indegree;
// 임의로 그래프 생성하는 Method
// 그래프 생성은 상황에 따라 유연하게 구현하면 됨
public void create_graph(int V){
this.V = V;
this.adj = new ArrayList<>();
this.indegree = new int[V]; // 내차수값 설정을 위한 배열
// 리스트 내에 리스트를 생성
// 인접 리스트 방식의 그래프 구현
for(int i=0; i < V; i++){
this.adj.add(new ArrayList<>());
}
}
// Graph의 정점 간 연결을 수행하는 Method
public void add_edge(int source, int target){
if(source > this.V || target > this.V){
throw new NullPointerException();
}
// source에 target으로의 방향성을 갖는 간선 추가
this.adj.get(source).add(target);
this.indegree[target]++; // 내차수값 증가(target이 대상이므로 target에 추가)
this.E++; // 간선 개수 ++, 사실 여기서는 쓰이진 않음.
}
// 위상 정렬을 수행하는 method
public boolean topological_sort(int[] result){
// 현재 정점 크기의 bool 배열 추가
boolean[] visited = new boolean[this.V];
boolean[] beingVisited = new boolean[this.V];
Stack<Integer> stack = new Stack<>();
boolean sort_result = false;
// 기존에 방문을 진행하지 않았다면 recursion을 통해 stack에 추가한다.
for(int i=0; i < this.V; i++){
if(!visited[i]){
sort_result = this.recursion(i, stack, visited, beingVisited);
}
if(!sort_result){
break;
}
}
int index = 0;
if(sort_result){
while(!stack.isEmpty()){
result[index++] = stack.pop();
}
}
return sort_result;
}
// stack에 넣기 위해 자신이 가리키는 이전의 모든 정점을 우선적으로 stack에 넣는다.
private boolean recursion(int v, Stack stack, boolean[] visited, boolean[] beingVisited){
beingVisited[v] = true;
ArrayList<Integer> arrayList = this.adj.get(v);
// 초기에는 true로 설정. Cycle이 없다는 의미
boolean isNotCycle = true;
for(int target : arrayList){
// 이미 재귀 중에 쌓여 방문 중인 상태면 Cycle이 있는 상태임!
if(beingVisited[target]){
return false;
}
// 이전에 이미 방문했으면 또 추가하지 않도록 한다.
if(!visited[target]){
isNotCycle = recursion(target, stack, visited, beingVisited);
}
// false라면 Cycle이 발생해서 false로 return된 것임
if(!isNotCycle) return false;
}
stack.push(v);
visited[v] = true;
// Stack에 넣었으니 방문 중인 상태임을 해제
beingVisited[v] = false;
return true;
}
}
결과는 다음과 같다.
5, 4, 2, 3, 1, 0,
Cycle이 발생했습니다!
Process finished with exit code 0
5. Backtracking을 통한 모든 경우의 수 구하기
※ 백트래킹(Backtracking) 이란?
백트래킹은 알고리즘의 기술적 요소로 그래프 상에서 탐색을 수행 시에 특정 조건을 만족하지 않으면 중간에 탐색을 중지하고 이전의 상태로 되돌아가도록 하는 것을 의미한다.
보통 그래프 탐색 중, 모든 경우의 탐색 가능한 경우를 구하고자 한다면 시간복잡도가 O(V+E)이므로 그 수에 따라 오랜 시간이 걸릴 수 있다.
그런데, 탐색 중 특정 조건이 만족하지 않는 경우에는 현재의 추가 탐색을 중지하고 다른 탐색 가능한 정점을 바로 찾아간다면 일부 탐색에 대해서는 배제가 가능하여 전체 탐색 시간이 단축될 것이다.
이러한 경우와 같이 특정 조건을 이용해 전체 탐색 성능을 효율적으로 수행하는 기법이라고 보면 된다. DFS 등 재귀적인 방식으로 탐색 시에 자주 사용된다.
이 백트래킹을 이용하여 위상 정렬의 모든 가능한 경우의 수를 찾을 수 있다. 탐색을 중지하는 조건은 현재 정점이 이미 방문이 완료된 경우라고 볼 수 있다.
원리는 다음과 같다.
① 반복문을 통해 정점을 돌며 내차수가 0인 정점에서 시작하고 방문 상태로 변경한 뒤 Stack에 넣는다.
② 시작 정점이 가리키는 다음 정점이 기 방문 상태가 아니라면 그 정점을 기준으로 또 재귀적으로 순회한다.
③ 모든 정점이 방문 완료 시, Stack에서 하나씩 꺼내고 꺼내진 정점의 방문 여부를 리셋한다.
④ 최초 반복문이 완료될 때까지 위 과정을 반복한다.
package com.test;
import java.util.ArrayList;
import java.util.Stack;
public class Graph {
public static void main(String[] args){
Graph graph = new Graph();
graph.create_graph(5);
graph.add_edge(2, 3);
graph.add_edge(3, 1);
graph.add_edge(4, 0);
graph.add_edge(4, 1);
graph.add_edge(5, 0);
graph.add_edge(5, 2);
graph.all_topological_sort();
}
private int V; // 정점의 개수
private int E; // 간선의 개수
private ArrayList<ArrayList<Integer>> adj; // 그래프를 표현하는 인접 리스트
private int[] indegree;
// 임의로 그래프 생성하는 Method
// 그래프 생성은 상황에 따라 유연하게 구현하면 됨
public void create_graph(int V){
this.V = V;
this.adj = new ArrayList<>();
this.indegree = new int[V+1]; // 내차수값 설정을 위한 배열
// 리스트 내에 리스트를 생성
// 인접 리스트 방식의 그래프 구현
for(int i=0; i <= V; i++){
this.adj.add(new ArrayList<>());
}
}
// Graph의 정점 간 연결을 수행하는 Method
public void add_edge(int source, int target){
if(source > this.V || target > this.V){
throw new NullPointerException();
}
// source에 target으로의 방향성을 갖는 간선 추가
this.adj.get(source).add(target);
this.indegree[target]++; // 내차수값 증가(target이 대상이므로 target에 추가)
this.E++; // 간선 개수 ++, 사실 여기서는 쓰이진 않음.
}
// 위상 정렬을 수행하는 method
public int[] all_topological_sort(){
// 현재 정점 크기의 bool 배열 추가
boolean[] visited = new boolean[this.V+1];
Stack<Integer> stack = new Stack<>();
recursion(stack, visited);
int[] sort_result = new int[this.V+1];
int index = 0;
while(!stack.isEmpty()){
sort_result[index++] = stack.pop();
}
return sort_result;
}
//
private void recursion(Stack stack, boolean[] visited){
// 위상 정렬의 결과가 나왔는지 확인을 위한 변수
boolean flag = false;
// 반복을 통해 내차수가 0인 것을 Stack에 우선 넣어가며 시작
for(int i=0; i <= this.V; i++){
if(!visited[i] && indegree[i] == 0){
// 결과에 포함시키기 위해 Stack 추가가
visited[i] = true;
stack.push(i);
// 결과에 추가되었으니 내차수값 1씩 감소
for(int adjacent : this.adj.get(i)){
this.indegree[adjacent]--;
}
// 재귀를 통해 다음 내차수가 0인 것들을 모두 순회
recursion(stack, visited);
// 재귀를 돌고 돌아왔으니 방문했던 것을 리셋
visited[i] = false;
stack.pop();
for(int adjacent : this.adj.get(i)){
this.indegree[adjacent]++;
}
flag = true;
}
}
// 여기 왔다는 것은 반복문을 건너뛰었다는 것.
// 즉, flag = false라면 모든 순회를 마친 상태이므로 결과를 얻음
if(!flag){
stack.forEach(i -> System.out.print(i + " "));
System.out.println();
}
}
}
결과는 다음과 같다.
4 5 0 2 3 1
4 5 2 0 3 1
4 5 2 3 0 1
4 5 2 3 1 0
5 2 3 4 0 1
5 2 3 4 1 0
5 2 4 0 3 1
5 2 4 3 0 1
5 2 4 3 1 0
5 4 0 2 3 1
5 4 2 0 3 1
5 4 2 3 0 1
5 4 2 3 1 0
Process finished with exit code 0
해당 포스팅은 GeeksForGeeks를 참조하여 구성하였습니다.
긴 글 읽어주셔서 감사합니다. 댓글로 피드백 주시면 반영하도록 하겠습니다.
'자바 프로그래밍 > 자료구조(Data Structure)' 카테고리의 다른 글
| 자료구조 - 접미사 트리(Suffix Tree) (0) | 2021.01.02 |
|---|---|
| 자료구조 - 접미사 배열(Suffix array, 맨버-마이어스 알고리즘) (0) | 2020.12.30 |
| 자료구조 - 정렬 7 (Bucket) (0) | 2020.11.14 |
| 자료구조 - 정렬 6 (Radix) (0) | 2020.11.14 |
| 자료구조 - 정렬 5 (Counting) (0) | 2020.11.14 |

