반응형
관련글
완전 탐색 관련 포스팅은 여기를 참조
1. 개요
문제의 링크는 여기를 참조
문제의 내용은 아래의 더보기를 클릭하여 참조
NxM 크기의 종이에 숫자가 써져 있을 때, 정사각형 4개가 이어 붙혀진 폴리오미노(테트로미노)를 놓을 때, 그 합이 가장 큰 경우의 숫자를 구하는 문제
※ 폴리오미노
크기가 1x1인 정사각형을 여러 개 이어 붙힌 도형
※ 테트로미노
정사각형 4개를 이어 붙인 폴리오미노
2. 풀이
테트로미노의 경우의 수는 다음의 19가지 이다.
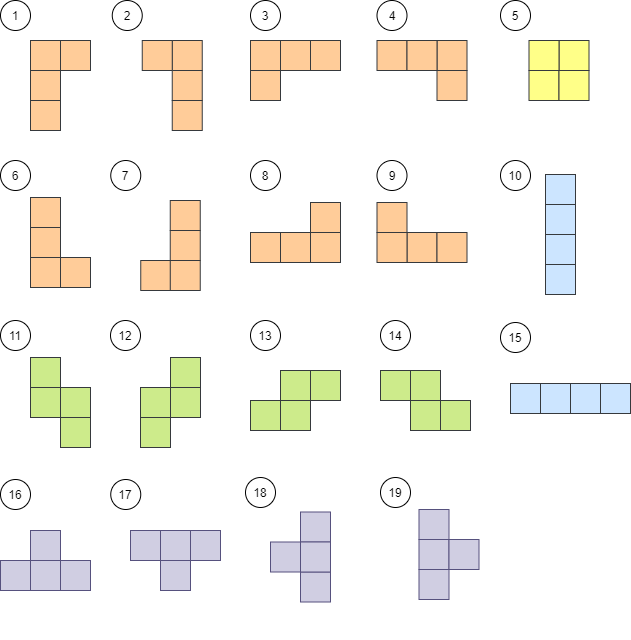
이 문제는 각 경우의 테트로미노에서 상단 좌측을 기준으로 종이에 놓는 19가지의 경우를 모두 체크하기만 하면 된다. 문제 자체는 크게 어려울 것 없지만 코드를 작성하는데 약간의 귀찮음이 따를 수 있다.
각 테트로미노를 놓을 때, 공간이 범위를 넘어서지 않는지를 생각하고 숫자를 더한 뒤 최대값을 구하면 정답을 알아낼 수 있다.
시간복잡도는 N과 M이 최대 500이므로 500x500의 위치에 19가지 경우의 수를 모두 테스트한다고 가정 시, 475,000가지 이므로 완전 탐색으로 가뿐히 풀 수 있다.
3. 코드
아래의 코드를 통해 정답을 알아보자.
import java.io.*;
public class Main{
static int n;
static int m;
static int[][] paper;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
String line[] = br.readLine().split(" ");
n = Integer.parseInt(line[0]);
m = Integer.parseInt(line[1]);
paper = new int[n][m];
for(int i=0; i < n; i++){
line = br.readLine().split(" ");
for(int j=0; j < m; j++){
paper[i][j] = Integer.parseInt(line[j]);
}
}
int max = 0;
for(int i=0; i < n; i++){
for(int j=0; j < m; j++){
max = Math.max(max, put(i, j));
}
}
bw.write(String.valueOf(max));
bw.flush();
br.close();
}
private static int put(int y, int x){
int ret_val = 0;
// 1번 테트로미노 : 우측, 아래측이 넘어가지 않는 지 확인
// ㅇㅇ
// ㅇ
// ㅇ
if(y+2 <= n-1 && x+1 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y][x+1] + paper[y+1][x] + paper[y+2][x]);
}
// 2번 테트로미노 : 우측, 아래측이 넘어가지 않는 지 확인
// ㅇㅇ
// ㅇ
// ㅇ
if(y+2 <= n-1 && x+1 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y][x+1] + paper[y+1][x+1] + paper[y+2][x+1]);
}
// 3번 테트로미노 : 우측, 아래측이 넘어가지 않는 지 확인
// ㅇㅇㅇ
// ㅇ
if(y+1 <= n-1 && x+2 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y][x+1] + paper[y][x+2]);
}
// 4번 테트로미노 : 우측, 아래측이 넘어가지 않는 지 확인
// ㅇㅇㅇ
// ㅇ
if(y+1 <= n-1 && x+2 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y][x+1] + paper[y][x+2] + paper[y+1][x+2]);
}
// 5번 테트로미노 : 우측, 아래측이 넘어가지 않는 지 확인
// ㅇㅇ
// ㅇㅇ
if(y+1 <= n-1 && x+1 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y][x+1] + paper[y+1][x+1]);
}
// 6번 테트로미노 : 우측, 아래측이 넘어가지 않는 지 확인
// ㅇ
// ㅇ
// ㅇㅇ
if(y+2 <= n-1 && x+1 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y+2][x] + paper[y+2][x+1]);
}
// 7번 테트로미노 : 좌측, 아래측이 넘어가지 않는 지 확인
// ㅇ
// ㅇ
// ㅇㅇ
if(y+2 <= n-1 && x-1 >= 0){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y+2][x] + paper[y+2][x-1]);
}
// 8번 테트로미노 : 좌측, 아래측이 넘어가지 않는 지 확인
// ㅇ
// ㅇㅇㅇ
if(y+1 <= n-1 && x-2 >= 0){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y+1][x-1] + paper[y+1][x-2]);
}
// 9번 테트로미노 : 우측, 아래측이 넘어가지 않는 지 확인
// ㅇ
// ㅇㅇㅇ
if(y+1 <= n-1 && x+2 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y+1][x+1] + paper[y+1][x+2]);
}
// 10번 테트로미노 : 아래측이 넘어가지 않는 지 확인
// ㅇ
// ㅇ
// ㅇ
// ㅇ
if(y+3 <= n-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y+2][x] + paper[y+3][x]);
}
// 11번 테트로미노 : 우측, 아래측이 넘어가지 않는 지 확인
// ㅇ
// ㅇㅇ
// ㅇ
if(y+2 <= n-1 && x+1 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y+1][x+1] + paper[y+2][x+1]);
}
// 12번 테트로미노 : 좌측, 아래측이 넘어가지 않는 지 확인
// ㅇ
// ㅇㅇ
// ㅇ
if(y+2 <= n-1 && x-1 >= 0){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y+1][x-1] + paper[y+2][x-1]);
}
// 13번 테트로미노 : 좌측, 우측, 아래측이 넘어가지 않는 지 확인
// ㅇㅇ
// ㅇㅇ
if(y+1 <= n-1 && x-1 >= 0 && x+1 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y][x+1] + paper[y+1][x] + paper[y+1][x-1]);
}
// 14번 테트로미노 : 우측, 아래측이 넘어가지 않는 지 확인
// ㅇㅇ
// ㅇㅇ
if(y+1 <= n-1 && x+2 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y][x+1] + paper[y+1][x+1] + paper[y+1][x+2]);
}
// 15번 테트로미노 : 우측이 넘어가지 않는 지 확인
// ㅇㅇㅇㅇ
if(x+3 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y][x+1] + paper[y][x+2] + paper[y][x+3]);
}
// 16번 테트로미노 : 좌, 우, 아래측이 넘어가지 않는 지 확인
// ㅇ
// ㅇㅇㅇ
if(y+1 <= n-1 && x-1 >= 0 && x+1 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y+1][x-1] + paper[y+1][x+1]);
}
// 17번 테트로미노 : 좌, 우, 아래측이 넘어가지 않는 지 확인
// ㅇㅇㅇ
// ㅇ
if(y+1 <= n-1 && x-1 >= 0 && x+1 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y][x+1] + paper[y][x-1] + paper[y+1][x]);
}
// 18번 테트로미노 : 좌, 아래측이 넘어가지 않는 지 확인
// ㅇ
// ㅇㅇ
// ㅇ
if(y+2 <= n-1 && x-1 >= 0){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y+2][x] + paper[y+1][x-1]);
}
// 19번 테트로미노 : 좌, 우, 아래측이 넘어가지 않는 지 확인
// ㅇ
// ㅇㅇ
// ㅇ
if(y+2 <= n-1 && x+1 <= m-1){
ret_val = Math.max(ret_val, paper[y][x] + paper[y+1][x] + paper[y+2][x] + paper[y+1][x+1]);
}
return ret_val;
}
}
읽어주셔서 감사합니다. 오류가 있으면 지적해주시면 반영하겠습니다.
반응형
'알고리즘 풀이(Problem Solving) > 완전 탐색(Brute Force)' 카테고리의 다른 글
| 알고리즘 풀이 - 백준 1748(수 이어 쓰기1, 완전 탐색) (0) | 2021.01.31 |
|---|---|
| 알고리즘 풀이 - 백준 6064(카잉 달력, 완전 탐색) (0) | 2021.01.31 |
| 알고리즘 풀이 - 백준 1107(리모컨, 완전 탐색) (0) | 2021.01.30 |
| 알고리즘 풀이 - 백준 1476(날짜 계산, 완전 탐색) (0) | 2021.01.26 |
| 알고리즘 풀이 - 백준 3085(사탕 게임, 완전 탐색) (0) | 2021.01.26 |


