관련글
Dynamic Programming 관련 포스팅은 여기를 참조
비슷한 문제인 9095번(1, 2, 3 더하기) 포스팅은 여기를 참조
1. 문제
문제 링크는 여기를 참조
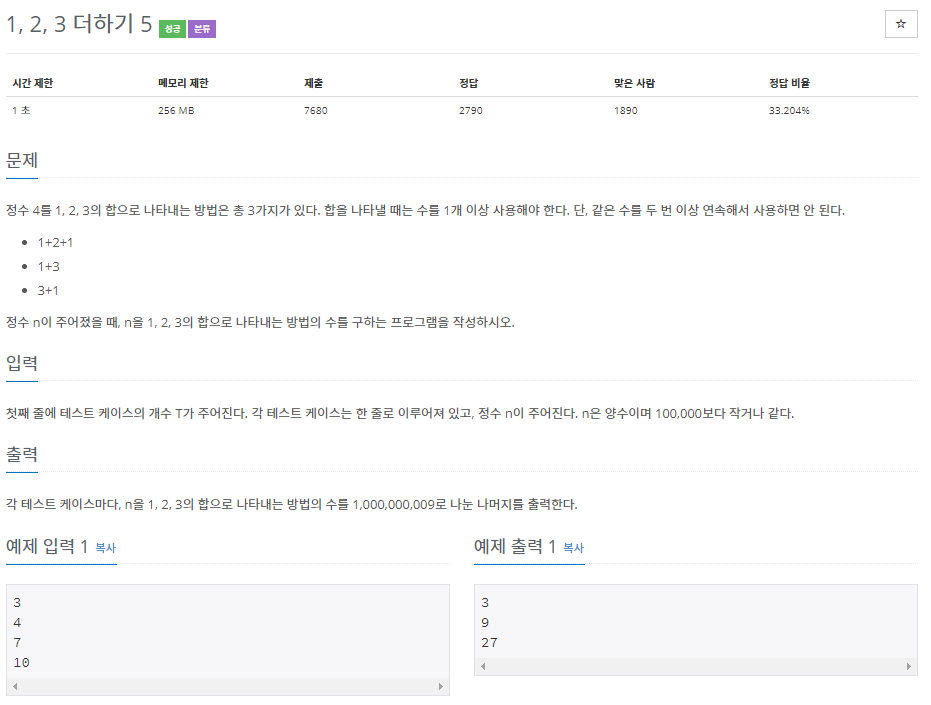
문제의 내용을 보려면 아래 더보기 클릭
이 문제는 1, 2, 3을 더해 N을 만드는 것은 동일하나 연속된 숫자를 사용할 수 없다.
2. 풀이
이 문제는 비슷한 문제인 9095번과 마찬가지로 DP로 해결 가능하다.
하지만 이전에는 State를 나타내는 N의 값만 변수로써 동작시키도록 값을 저장하였지만 이번에는 가장 최근에 사용된 값이 1, 2, 3중 어느 것이었는지도 알아야 한다.
따라서, State를 저장하는 배열이 2차원으로 생성되어야 한다. 즉, DP[N][1], DP[N][2], DP[N][3]과 같이 N*3의 배열을 만들어야 한다.(Index 고려하면 N+1 * 4)
각 부분이 의미하는 바는 다음과 같다.
DP[N][1] : N이라는 숫자를 1, 2, 3으로 만드는 데 마지막에 1을 더한 경우
DP[N][2] : N이라는 숫자를 1, 2, 3으로 만드는 데 마지막에 2를 더한 경우
DP[N][3] : N이라는 숫자를 1, 2, 3으로 만드는 데 마지막에 3을 더한 경우
예를 들어서, 5를 나타낸다고 해보자.
DP[5][1]의 경우의 수 : (1+3+1)의 1가지
DP[5][2]의 경우의 수 : (3+2, 2+1+2)의 2가지
DP[5][3]의 경우의 수 : (2+3)의 1가지
즉, 5를 만드는 방법은 총 4가지가 되는 것이다.
이 때, 각 DP[N][i]는 다음과 같이 계산이 가능하다.
DP[N][1] = SUM(DP[N-1][2], DP[N-1][3])
DP[N][2] = SUM(DP[N-2][1], DP[N-2][3])
DP[N][3] = SUM(DP[N-3][1], DP[N-3][2])
따라서, 작은 문제들인 DP[N-3], DP[N-2], DP[N-1]을 반복하여 사용하고 해당 최적 결과값이 그대로 사용되므로 DP의 두 가지 조건인 Overlapping Subproblems와 Optimal Substructure를 만족한다.
그렇다면, DP로 풀 수 있으니 저장할 State의 정의를 한 번 세워보자. 아래와 같을 것이다.
정의 : DP[N] = N을 1, 2, 3의 합으로 나타내되 중복된 숫자를 연속으로 쓰지 않는 방법의 수
기저 상태와 점화식을 세워보자.
기저 상태는 n이 1, 2, 3의 경우일 것이다. 다음과 같다.
기저 상태 :
DP[1][1] = 1, DP[1][2] = DP[1][3] = 0
DP[2][1] = 0, DP[2][2] = 1, DP[2][3] = 0
DP[3][1] = 1, DP[3][2] = 1, DP[3][3] = 1
점화식은 아래와 같다.
점화식 :
DP[N][1] = DP[N-1][2] + DP[N-1][3]
DP[N][2] = DP[N-2][1] + DP[N-2][3]
DP[N][3] = DP[N-3][1] + DP[N-3][2]
3. 코드
아래의 코드를 통해 정답을 알아보자.
1) Bottom-up 방식
import java.io.*;
public class Main{
static final long MOD = 1000000009;
static long[][] dp;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
// 문제에서 최대 100,000까지만 나오므로 미리 모두 계산함!
bottomUp(100000);
for(int i=0; i < T; i++){
int n = Integer.parseInt(br.readLine());
long result = ((dp[n][1] + dp[n][2]) % MOD + dp[n][3]) % MOD;
bw.write(String.valueOf(result)+"\n");
}
br.close();
bw.flush();
}
// Bottom-up 방식
public static void bottomUp(int n){
dp = new long[n+1][4];
// 기저 상태는 1, 2, 3을 각각 나타내는 방법의 수
dp[1][1] = dp[2][2] = dp[3][1] = dp[3][2] = dp[3][3] = 1;
// 반복문을 통해 점화식을 구성하여 최소값을 채워나감
for(int i=4; i <= n; i++){
dp[i][1] = (dp[i-1][2] + dp[i-1][3]) % MOD;
dp[i][2] = (dp[i-2][1] + dp[i-2][3]) % MOD;
dp[i][3] = (dp[i-3][1] + dp[i-3][2]) % MOD;
}
}
}
2) Top-Down 방식
아래와 같이 구현하였는데, Bottom-up 방식과 비교한 결과 정답은 맞지 않을까 생각하지만 StackOverflow가 나서 틀린 것으로 나오는 듯 하다.
방법을 알아내면 추후 업데이트를 진행하도록 하겠습니다.
import java.io.*;
public class Main{
static int MOD = 1000000009;
static long[][] dp;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
dp = new long[100001][4];
dp[1][1] = dp[2][2] = dp[3][1] = dp[3][2] = dp[3][3] = 1; // 기저 상태는 1, 2, 3을 나타내는 방법의 수
// 미리 모두 계산 완료함
for(int i=1; i <= 3; i++){
topDown(100000, i);
}
for(int i=0; i < T; i++){
int n = Integer.parseInt(br.readLine());
long result = ((dp[n][1] + dp[n][2]) % MOD + dp[n][3]) % MOD;
bw.write(result + "\n");
}
br.close();
bw.flush();
}
// Top-down 방식
public static long topDown(int n, int idx){
if(n == 1 || n == 2 || n == 3) return dp[n][idx];
if(dp[n][idx] > 0) return dp[n][idx]; // 이전에 계산 되었으면 반환
for(int i=1; i <= 3; i++){
if(i != idx){
dp[n][i] = (dp[n][i] + topDown(n-1, i)) % MOD;
}
}
return dp[n][idx];
}
}
읽어주셔서 감사합니다. 오류가 있으면 지적해주시면 반영하겠습니다.
'알고리즘 풀이(Problem Solving) > Dynamic Programming' 카테고리의 다른 글
| 알고리즘 풀이 - 백준 2193(이친수, DP) (0) | 2021.01.08 |
|---|---|
| 알고리즘 풀이 - 백준 10844(쉬운 계단 수, DP) (0) | 2021.01.08 |
| 알고리즘 풀이 - 백준 16194(카드 구매하기 2, DP) (0) | 2021.01.07 |
| 알고리즘 풀이 - 백준 11052(카드 구매하기, DP) (0) | 2021.01.07 |
| 알고리즘 풀이 - 백준 9095(1,2,3 더하기, DP) (0) | 2021.01.06 |