관련글
Dynamic Programming 관련 포스팅은 여기를 참조
1. 개요
문제 링크는 여기를 참조
문제의 내용을 보려면 아래 더보기 클릭
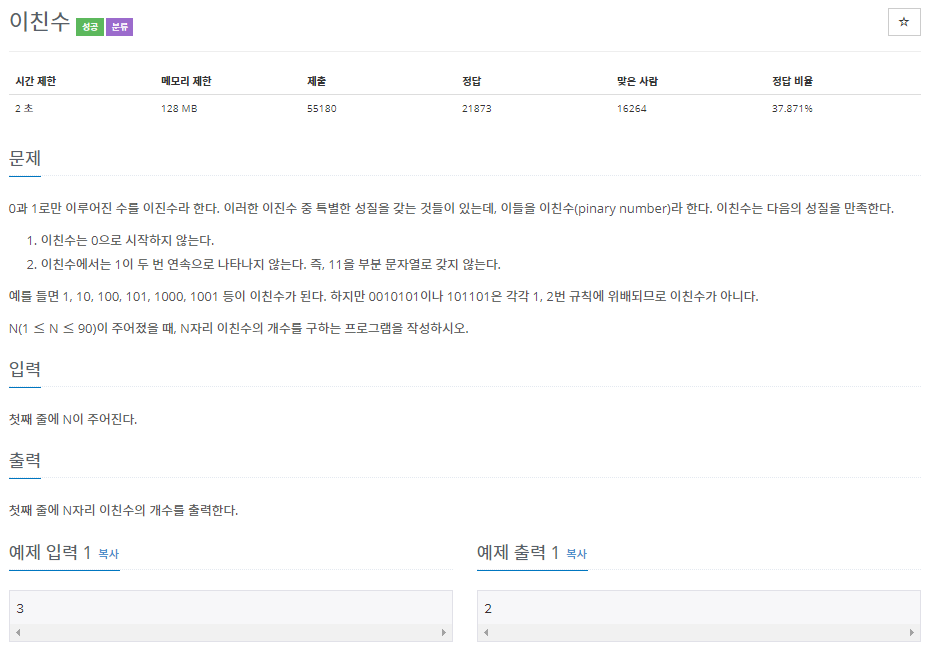
길이 N이 주어질 때, N 길이의 이친수의 개수를 구하는 프로그램
이친수란?
0으로 시작하지 않으며, 1이 연속으로 오지 않는 0, 1로만 이루어진 수. ex) 10010 ( O ), 1101 ( X )
2. 풀이
이 문제는 DP로 풀 수 있다.
이전의 포스팅인 계단 수를 구하는 경우와 비슷하지만 이전의 수가 0 또는 1의 State로만 지정된 것이다.
여기서 State는 숫자의 길이인 N과 N-1번째 숫자가 0 또는 1 경우의 2가지이다.
2차원의 State를 저장하는 배열을 기반으로 각 부분이 의미하는 바는 아래와 같다.
DP[N][0] = DP[N-1][0] + DP[N-1][1]
DP[N][1] = DP[N-1][0]
위를 기반으로 만들 수 있으며, 각 부분에서 DP[N-1][i]가 반복적으로 사용되고 해당 최적 결과값이 그대로 사용되니 DP의 두 가지 조건인 Overlapping Subproblems와 Optimal Substructure를 만족한다.
그렇다면, DP로 풀 수 있으니 저장할 State의 정의를 한 번 세워보자. 아래와 같을 것이다.
정의 : DP[N][i] = 길이 N의 계단 숫자 중 i로 끝나는 숫자의 개수
기저 상태를 알아보자.
기저 상태는 맨 첫번째 자리의 숫자를 결정하는 경우일 것이다. 우선 0으로 시작하는 것은 불가하다.
기저 상태 :
DP[1][0] = 0
DP[1][1] = 1
3. 코드
아래의 코드를 통해 정답을 알아보자.
1) Bottom-up 방식
import java.io.*;
public class Main{
static long[][] dp;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
bottomUp(N);
long result = 0;
for(int i=0; i < 2; i++){
result += dp[N][i];
}
bw.write(String.valueOf(result) + "\n");
br.close();
bw.flush();
}
// Bottom-up 방식
public static void bottomUp(int n){
dp = new long[n+1][2];
// 기저 상태는 길이 1의 숫자를 나타내는 방법의 수
dp[1][1] = 1;
// 반복문을 통해 점화식을 구성하여 최소값을 채워나감
for(int i=2; i <= n; i++){
// 0, 9로 끝나면 1, 8로 끝나는 수 뒤에만 붙일 수 있다.
dp[i][0] = dp[i-1][1] + dp[i-1][0];
dp[i][1] = dp[i-1][0];
}
}
}
2) Top-Down 방식
import java.io.*;
public class Main{
static long[][] dp;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
// 기저 상태는 길이 1의 숫자를 나타내는 방법의 수(1~9까지)
dp = new long[N+1][2];
dp[1][1] = 1;
for(int i=0; i < 2; i++){
topDown(N, i);
}
long result = 0;
for(int i=0; i < 2; i++){
result += dp[N][i];
}
bw.write(String.valueOf(result) + "\n");
br.close();
bw.flush();
}
// Top-Down 방식
public static long topDown(int n, int k){
if(dp[n][k] > 0 || n == 1) return dp[n][k]; // 값이 있거나 n이 1이면 반환
if(k == 0) return dp[n][k] = topDown(n-1, 0) + topDown(n-1, 1);
else return dp[n][k] = topDown(n-1, 0);
}
}
읽어주셔서 감사합니다. 오류가 있으면 지적해주시면 반영하겠습니다.
'알고리즘 풀이(Problem Solving) > Dynamic Programming' 카테고리의 다른 글
| 알고리즘 풀이 - 백준 14002(가장 긴 증가하는 부분 수열 4, DP) (0) | 2021.01.11 |
|---|---|
| 알고리즘 풀이 - 백준 11053(가장 긴 증가하는 부분 수열, DP) (2) | 2021.01.11 |
| 알고리즘 풀이 - 백준 10844(쉬운 계단 수, DP) (0) | 2021.01.08 |
| 알고리즘 풀이 - 백준 15990(1, 2, 3 더하기 5, DP) (0) | 2021.01.07 |
| 알고리즘 풀이 - 백준 16194(카드 구매하기 2, DP) (0) | 2021.01.07 |